Conway's game of life Software!!

ライフゲームとは

まだ一日も経っていないですが、ソフトウェアを更新しました(9/21)

ライフゲームソフトウェアを製作しました!!!
ライフゲーム(Conway's game of life)とは...

ライフゲームとは2次元のセルオートマトンである。
n✕mのマスがあり、
白色状態を死、黒色状態を生とするならば、
生コマの周りに生コマが2〜3コマあるならば、そのコマは生き続ける。
死コマの周りに生コマが3コマあるならば、そのコマは復活する。
その他の条件のとき、そのコマは、死亡する。
つまり、程度な人数が周りにいれば、生まれ、
多すぎてもダメ、少なすぎても寂しくて死んでしまうというものである。

このようなルールに基づき、シミュレーションを行うのが、ライフゲームである。

このように、通常は、死→生(Born)が3、生→生(Survives)が2,3となっています。
これをB3/S23と表記します。
この標準ルールを含む様々なルールでシミュレーションを行います。
実装言語はRです。

ソフトウェア仕様

シミュレーションしよう、、の前にソフトウェアの仕様を説明します。
このソフトウェアの特徴を列挙します。

任意のマップのマス数を指定することができます
マスを全て生状態・全て死状態・ランダムから任意に選択することができます
手動でパターンを生成することができます。
変更したいパターン数を入力し、その数だけ変更することができます
変更方法は、マウスクリックで直感的に操作することができます
パターンを選択できます
パターンは、nomal/day and night/HighLife/Replicator/2x2があります
また、その他の場合は、[B(a),B(b) S(c),S(d)]という表記で規則を与えることができます
例えば、nomalであれば、[3 3,4]といった感じです
収束判別モードを~~選択できます~~自動実行します
これは、収束が第何世代で起きたかを調べるモードです
~~ただし、この処理は、多少動作が重くなるため、任意で選択しないことも可能です~~
アルゴリズムを変更し、オーダーが大幅に減少したため、常時収束判定を行います
世代ステップ実行ができます
エンターキーで順次ステップ実行します
ステップ数を指定することでその世代までを自動的に実行します
(無限実行は速すぎてよく見えない上にマシン性能が足りない)

UIがキレイになりました
今までは白→死、緑→生でしたが、
黒→死、緑→生にすることで見た目がキレイになりました
こんな感じ
f:id:meriyasu_blog:20150921034558p:plain

処理高速化を図り、ビットボードを実装しようとしましたが、
R言語はデフォルトではビット演算ができないため、断念しました。
よって、計算量はおおよそ8(m✕n)です。
アルゴリズムを変更し、計算量は3/2(m✕n)程度(変動あり)になりました。
いつかはビットボードを実装したいです。

ソースコードはGitHubにて公開します。
MITライセンスです
github.com

シミュレーション

まずは、通常のライフゲームのシミュレーションから。
マップはランダムです。
初期位置はこのようになっています。
f:id:meriyasu_blog:20150920204728p:plain

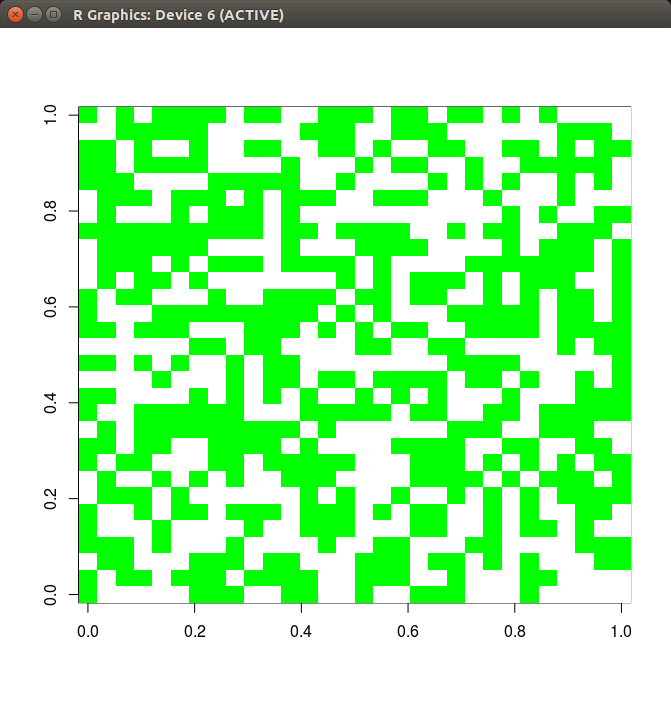
次に431世代後

f:id:meriyasu_blog:20150920204652p:plain

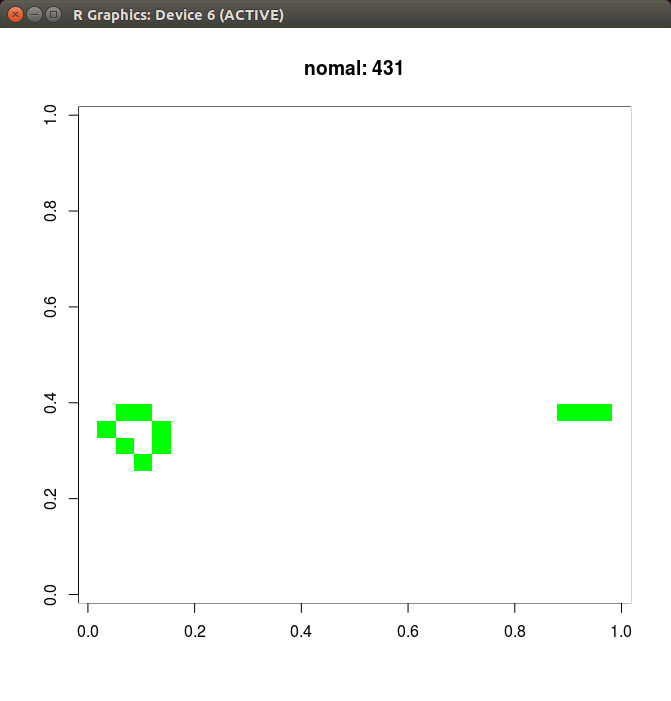
固定子や振動子ができ、収束しました。

Day and night

B3678/S34678
密度が高いところを生存しやすく、密度が低いところは絶滅しやすい特徴をもちます。。
ランダムに生成されたマップにおいて最も変化を楽しめる規則といえます。
Day and Night (cellular automaton) - Wikipedia

初期マップはランダムで与え、シミュレーションするとこのようになりました。
f:id:meriyasu_blog:20150920195902p:plain
今回の場合は、密度がどこも高かったようで、
688世代後、振動子のみが死状態となりました。
何度もやってみましたが、どうやら50✕50のマップでは、狭すぎるようで、
どれも、ほとんど生状態になりました。
そこで、マス数を増やし、100✕100でシミュレーションしてみました。
すると、このようになりました。
f:id:meriyasu_blog:20150920200506p:plain
317世代程度で見事に大陸ができました。
世代数を増やせば、もっとまとまりができるでしょう。

HighLife

B36/S23
特定の形を自己複製する機能をもつ規則です。
Highlife (cellular automaton) - Wikipedia

これは特定の形を初期状態として与えてみます。
f:id:meriyasu_blog:20150920200932p:plain
これを初期状態にして、世代を進めます。すると12世代目で、

2体に複製されました！
進めていくと、36世代で、
f:id:meriyasu_blog:20150920201023p:plain
4体に複製されました。
このような特徴を持ちます。
また、この他の形は、複製されません。