Memorandums?

This blog is written about technical-discoveries and daily-events.

Top > 電験3種

発電所の効率的運用 19th-day

電験3種

Commentary.

様々な発電方法が存在するが、それぞれに向き不向きがある。
電源設備は、日負荷曲線分担部分に応じて、3種類に大別される。

ピーク供給力

  • 急激な出力変化
  • 頻繁な始動・停止
  • 運転費は高くてもよいが、建設費は安く
ex. 揚水式発電・石油火力発電

中間供給力

  • 始動・停止・負荷調整
  • ピーク・ベースの中間的存在
ex. LNG火力発電

ベース供給力

  • 長時間の継続運転
  • 始動・停止には時間を要しても良い
  • 建設費は高くてもよいが、高利用率・経済性の高いもの
ex. 一般水力発電・原子力発電・石炭火力発電
水力発電は、始動・停止は非常に短時間でしうるが、
流込み式でなければ、安定供給が可能となる。


次に発電原価についてである。
発電原価は、1kWhあたりの経費のことをいう。
内訳としては、大別して、固定費と燃料費の2つであり、
{ 発電原価 = \frac{固定費+燃料費}{発生電力量 \ kWh} }
燃料費以外の運転関連の経費は僅かであるため、
建設費に経費率を掛けることによって求める。
{ 発電原価 = \frac{建設費 \times 年経費率}{年間発生電力量} + 燃料費 \ 円/kWh }
{ 年間発生電力量 = 年間総時間数 \times 定格出力 \times 負荷率 }
{ \frac{建設費}{定格出力} = C, 年経費率 = \gamma, 負荷率 = L }
とするならば、固定費部分は、
{ \frac{建設費 \times 年経費率}{年間発生電力量} = \frac{建設費 \times 年経費率}{年間総時間数 \times 定格出力 \times 負荷率} = \frac{\frac{建設費}{定格出力} \times 年経費率}{年間総時間数 \times 負荷率} = \frac{C \gamma}{8760h \times L} }

燃料費は、必要とするエネルギーは、
{ 定格出力 = P, 熱効率 = \eta }
とするならば、
{ \frac{P \times 8760(年間総時間数)}{\eta} }
熱量で表すと、
1kWh = 3600kJなので、
{ \frac{P \times 8760 \times 3600}{\eta} }
であり、使用燃料の発生熱量あたりの単価をf[円/kJ]とすると、燃料費は、
{ 燃料費 = \frac{P \times 8760 \times 3600 \times \frac{f}{\eta}}{P \times 8760} = \frac{3600f}{\eta} }

固定費と燃料費を合わせた発電原価[円/kWh]は、
{ 発電原価 = \frac{C \gamma}{8760 \times L} + \frac{3600f}{\eta} }
となる。
水力発電では、燃料費を0とし、原子力発電では、燃料費を核燃料費と置き換えれば、適用できる。

Consideration.

それぞれの発電方法にどのような特徴があるかをつかむ必要がある。
火力発電には、さまざまな分類があり、ひとくくりに特徴はつかめない。
発電原価については、ややこしい。
固定費→建設費
燃料費→燃料費(そのまま)
と置き換えて考えなくてはいけない。

制御工学part1 過渡応答 18th-day

制御工学 電験3種

Question.

下図で構成される回路に、ヘビサイド関数に従った電圧v(t)を与える。
このときの電流i(t)の特性を求めよ。
f:id:meriyasu_blog:20150307130734p:plain:w200

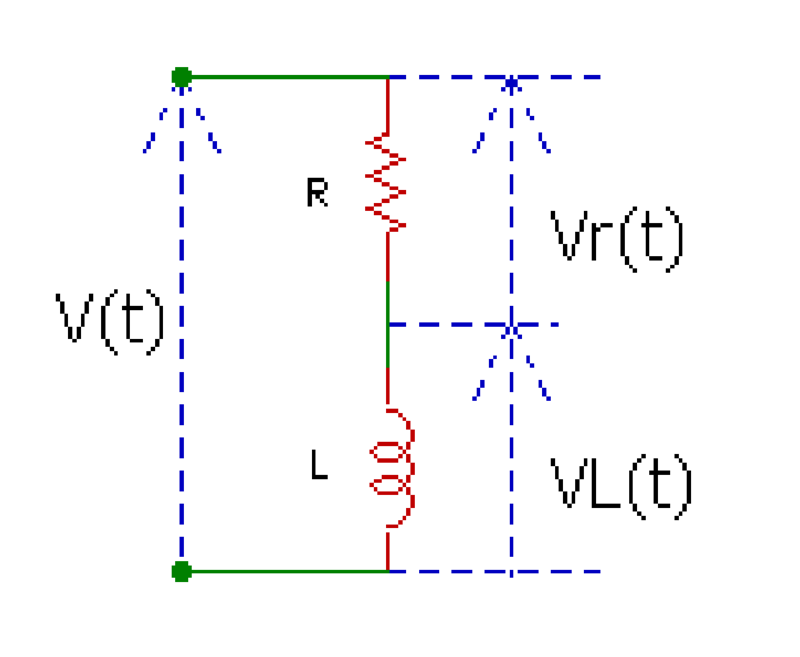
Solver.

制御工学の基礎、過渡応答の問題である。
ただし、この問題は、電験3種では、出ない可能性が高い。

制御工学とは、

入力と出力の関係を示す伝達関数を用いることによって、
その入出力システムの挙動及び、パフォーマンスを評価するための学問である。

と定義される。
制御工学では、
時間領域に存在する、元となる方程式・入力信号をラプラス変換によって、
複素数領域に持ち込み、処理をしたのちに逆フーリエ変換を用いて、時間領域に戻すことによって、
出力の挙動を得ることができる。

複素数領域に持ち込む手法の一つであるラプラス変換とは、次式によって定義される。
{ F(s) = \int_{0}^{\infty}f(t)e^{-st}dt \\ ただし、s = \sigma + j \omegaとする。 }
また、逆ラプラス変換は、次式によって定義される。
{ f(t) = \frac{1}{2 \pi j} \int_{c-j \infty}^{c+j \infty}F(s)e^{st}ds }
これらの定義式を毎回使うのは、大変であるため、通常は、ラプラス変換表という表を用いて、計算を行う。
抜粋したフーリエ変換表をTable1に示す。

Table1. フーリエ変換表(一部抜粋)
f(t) F(s)
1 { \delta (t) = \left\{\begin{array}{l} \infty \ \ \ t = 0 \\ 0 \ \ \ \ t \neq 0 \end{array}\right. } (インパルス関数) 1
2 { u(t) = \left\{\begin{array}{l} t < 0 \ \ \ u(t)=0 \\ t \geq 0 \ \ \ u(t)=1 \end{array}\right. } (ヘビサイド関数) \frac{1}{s}
3 e^{-at} \frac{1}{s+a}
4 f'(t) sF(s)-f(0)
5 \int_{0}^{t}f(t)dt \frac{1}{s}F(s)

これらを使い、変換していく。
では、回路素子について、ラプラス変換を考えていく。

抵抗のラプラス変換

抵抗は、オームの法則より、以下の式で表される。
v(t) = R \times i(t)
よって、フーリエ変換を行うと、
{ \left\{\begin{array}{l} V(s) = R \times I(s) \\ I(s) = \frac{1}{R} \times V(s) \end{array}\right. }
となる。

容量のラプラス変換

キャパシタの関係式は次のようにあらわされる。
v(t) = \frac{1}{C} \times q(t)
また、電流は微小時間当たりの電荷量であるので、
i(t) = \frac{dq(t)}{dt}
よって、
i(t) = C \frac{dv(t)}{dt}
v(t) = \frac{1}{C} \int i(t)dt
v(t)をラプラス変換表5番によって、ラプラス変換すると、
v(t) = \frac{1}{C} \int i(t)dt \Leftrightarrow V(s) = \frac{1}{sC} I(s)
I(s) = sCV(s)
となる。

インダクタのラプラス変換

インダクタの定義式は、
微小時間当たりの電流の変化量が電圧に比例し、比例定数をLとするので、
v(t) = L \frac{di(t)}{dt}
v(t)をラプラス変換表4番によって、ラプラス変換すると、
v(t) = L \frac{di(t)}{dt} \Leftrightarrow V(s) = sLI(s)
I(s) = \frac{1}{sL}V(s)
となる。

電気回路における出力信号の求め方を説明する。

  1. 回路方程式を求める
  2. 回路方程式をラプラス変換により、複素数領域に持ち込む
  3. 入力信号をラプラス変換により、複素数領域に持ち込む
  4. 回路方程式と入力信号を複素数領域において、掛け合わせる
  5. 逆ラプラス変換によって、時間領域に戻す
このような手順で出力を求めることができる。
では、早速、順番通りに解いていく。
回路方程式
直列RL回路の電圧を考える。
抵抗による電圧降下 v_rは、
v_r (t) = R \times i(t)
インダクタによる電圧降下 v_lは、
v_l (t) = L \frac{di(t)}{dt}
よって、起電力 v(t) は、
v(t) = v_r + v_l = R i(t) + L \frac{di(t)}{dt}
回路方程式のラプラス変換
さきほどの抵抗とインダクタのラプラス変換を用いて、ラプラス変換を行うと、
{ v(t) = R i(t) + L \frac{di(t)}{dt} \\ \Leftrightarrow V(s) = \mathcal{L}[Ri(t)] + \mathcal{L} \left[L\frac{di(t)}{dt} \right] = RI(s) + sLI(s) = (R+sL)I(s) }
よって、
I(s) = \frac{1}{R+sL} V(s)
入力信号のラプラス変換
入力信号は、ヘビサイド関数であるため、
ヘビサイド関数を u(t)とおくと、そのラプラス変換は、
\mathcal{L}[u(t)] = \frac{1}{s}
となる。
t \geq 0のときの電圧値を V_0とすると、
\mathcal{L}[V_0 \times u(t)] = \frac{V_0}{s}
となる。
複素数領域での回路方程式と入力信号の融合
入力電圧信号を回路方程式に代入する。
つまり、 V(s) = \frac{V_0}{s}である。
そして、逆フーリエ変換しやすい形へと変形していく。
{ I(s) = \frac{1}{R+sL} \times \frac{V_0}{s} = \frac{V_0}{sR+s^2 L} \\ = \frac{V_0}{s(R+sL)} = \frac{V_0}{L} \times \frac{1}{s \left(\frac{R}{L}+s \right)} }
ここで、部分分数分解を行う。
{ \frac{1}{s(\frac{R}{L}+s)} = \frac{A}{s}+\frac{B}{\frac{R}{L}+s} \\ \frac{A \frac{R}{L} + As + Bs}{s \left(\frac{R}{L}+s \right)} }
よって、
{ \left\{ \begin{array}{l} A \frac{R}{L} = 1 \\ A + B = 0 \end{array} \right. }
となり、
{ \left\{ \begin{array}{l} A = \frac{L}{R} \\ B = - \frac{L}{R} \end{array} \right. }
となるので、
{ \frac{1}{s(\frac{R}{L}+s)} = \frac{L}{R} \left(\frac{1}{s} - \frac{1}{s+\frac{R}{L}}\right) }
したがって、
I(s) = \frac{V_0}{R} \left(\frac{1}{s} - \frac{1}{s+\frac{R}{L}}\right)
ここで、 \frac{V_0}{R}及び、 \frac{R}{L}は定数であるので、
フーリエ変換表2, 3番を用いて、逆フーリエ変換を適用できる。
{ i(t) = \frac{V_0}{R} \left(\mathcal{L}^{-1} \left[\frac{1}{s} \right] - \mathcal{L}^{-1} \left[\frac{1}{s+\frac{R}{L}} \right]\right) \\ = \frac{V_0}{R}(1-e^{-\frac{R}{L}t}) }

f:id:meriyasu_blog:20150307214004p:plain:w300

Consideration.

今回は、制御工学基礎・ラプラス変換についての問題であった。
ラプラス変換の最大の利点は、複素数領域に持っていくことで、
出力を考えるときに難しい計算を行わなくてよくなるという面である。
複素数領域で計算された値自体には意味はないが、それを逆ラプラス変換によって、
出力信号という意味のある式を導き出すことができる。

しかし、これは、制御工学の本質ではなく、本質は、伝達関数である。
伝達関数については、のちほど。

電線の種類 17th-day

電験3種

Commentary.

電線には、様々な種類がある。
その中の一つに、複合ケーブルというものがある。
複合ケーブルとは、電線と電力保安通信線とを束ねたものの上に保護被膜を施したケーブルのことである。

また、他にもケーブルには、裸電線や絶縁電線があるが、これらの接続には決まりがある。

  • 電線の電気抵抗を増加させない接続方法であること。
  • 電線の引張り強さを20%以上減少させないこと。
  • 接続には、接続管および専用器具、ロウ付けすること。
  • 絶縁電線相互を接続する場合に、絶縁電線の絶縁物同等の絶縁効力のあるもので被覆すること。

また、ケーブル・キャブタイヤケーブル・コードを直接接続するには、条件がある。

  • 断面積 8{mm}^2以上のキャブタイヤケーブル
  • 金属被覆のないケーブル
このいずれかを満たすものは直接接続できる。
金属被覆のないケーブルとは、VVケーブルなどがある。

電線の強度に関して、
電気設備の保安のために施設する線は、通常の使用状態において、断線の恐れがないようにしなければいけない。
接続時には、電気抵抗の増加を抑え、絶縁性能の低下、通常使用状態での断線がないようにしなくてはいけない。

Consideration.

覚えるべき点は多いが、難易度の高い部分に絞って解説した。
ケーブルには、様々な種類があり、把握しにくいが、
電気抵抗の増加を抑える・断線しないようにするなど、常識的なことも多い。

電圧の種類 16th-day

電験3種

Question.

11.4kV/6.6kV三相4線式配電線の中性線と電圧線に接続される
6.6kV単相配電線の電圧区分は何か。

Solver.

電圧は、電圧の大小によって、低圧・高圧・特別高圧に区分される。
低圧は、交流では600V以下、直流では750V以下となり、
高圧は、低圧以上7000V以下、
特別高圧は、7000V以上となる。

機器製作の規格化、および、他送配電線との関連も考慮して、標準的な電圧値というものを定めている。
それが、公称電圧と最大電圧である。
公称電圧とは、電線路を代表する線間電圧のことをいい、
最高電圧とは、電線路に通常発生する最高線間電圧のことをいう。
耐圧試験電圧値の基準として、最大使用電圧も定めている。

  • 公称電圧1000V以下では、その1.15倍
  • 公称電圧1000V超え、500,000V未満では、その \frac{1.15}{1.1}倍
となっている。
一般的に、電路と大地との電位差を対地電圧というが、非接地式電路の場合は、線間電圧のことを対地電圧という。

問題では、
多線式電路の中性線と他の1線を電気的に接続している。
この場合、多線式電路の最大使用電圧が、他の1線の最大使用電圧と等しいと定められるため、
6.6kVではなく、11.4kVとして考えなくてはならない。
よって、11.4kVは、特別高圧となる。

Consideration.

今回から法規の内容に移行する。
電圧の分類については、そのままであるが、
実際に区分するときには、最大使用電圧を考とを忘れてはいけない。
また、多線式電路に接続する電線の電圧区分であっても、多線式電路の最大使用電圧を考えなくてはいけない。

後々も頻繁に必要となる知識であるため、しっかり押さえておきたい。

誘導電動機の等価回路 15th-day

電験3種

Question.

すべりsで回転するかご形三相誘導電動機がある。
スター形一次換算1相分の等価回路において、二次側枝路のインピーダンス \dot{{Z_2}'}を求めよ。

Solver.

かご形回転子の導体中に発生する誘導起電力は、すべりsに比例する。
周波数も同様である。
これは、回転磁界と回転子の回転速度の差によって、誘導起電力が生ずるためである。
すべりがない(s=0)ならば、差がないので、誘導起電力は生じないはずである。
また、100%すべり(s=1)ならば、差が大きく、大きな誘導起電力が生じるはずである。
よって、sが大きいほど、誘導起電力が生じる、つまり、比例するのである。
毎秒の回転数と言い換えることのできる周波数も同じことがいえる。

2次側誘導起電力は、 sE_2であり、
2次側インピーダンスは、 r_2 + js x_2である。
2次側電流を求めると、
I_2 = \frac{sE_2}{r_2 + js x_2} = \frac{E_2}{\frac{r_2}{s}+j x_2}
となり、
2次側インピーダンス \dot{{Z_2}'} = \frac{r_2}{s} + j x_2
となる。

Consideration.

すべりに対する誘導起電力や周波数の変化は、
実際にすべりが大きくなったとき・小さくなったときを考えれば、わかる。
インピーダンスは、 r_2 + js x_2ではなく、誘導起電力のことも考慮して、
\frac{r_2}{s} + j x_2 となることに注意である。

誘導電動機・発電機の構造 14th-day

電験3種

Commentary.

誘導機の仕組みについて考える。
固定子の励磁電流による同期速度の回転磁界と回転子との速度の差によって、
回転子に電圧が発生する。
その電圧によって、回転子に電流が流れる。
回転子の電流と磁束との間で発生するトルクを制御するため、巻線形の場合、
回転子巻線の回路をブラシとスリップリングで外部に引き出し、二次抵抗値を調整する。
回転子回転速度が0、すなわち滑りが1であるときから、同期速度、すなわち滑りが0であるときまでの
運転状態では、誘導機は、誘導電動機となる。
回転子の速度が同期速度よりも速い場合、誘導機は、誘導発電機として働く。

かご形三相誘導電動機のかご形回転子は、
棒状の導体の両端を端絡環に溶接・ロウ付けした構造になっている。
小容量～中容量の誘導電動機では、
導体・端絡環・通風翼が高純度のアルミニウムの加圧鋳造で作られた一体構造となっている。

Consideration.

今回重要な点は、
巻線形誘導機では、スリップリングとブラシによって、外部抵抗へと接続するという点。
かご形誘導機では、導体と端絡環と通風翼をアルミで一体製作するという点。
この2点となる。

誘導電動機の同期速度 13th-day

電験3種

Question.

6極の誘導電動機がある。
端子電圧をV[V]、周波数をf[Hz]とし、
V/f比=4で一定制御インバータで66Hzで駆動している。
すべりが5%であるとき、誘導電動機の回転速度 [ min^{-1} ]を求めよ。

Solver.

電動機は、三相交流を供給すると回転磁界が発生し、回転する仕組みとなっている。
磁極が、N-S一対であるとき、磁極数は、2極であるといい、
極数の半分の回数で1回転する。
1分間の回転数n [ min^{-1} ]を求める。極数をpとすると、
n = \frac{f}{\frac{1}{2}p} \times 60 = \frac{120f}{p}
となる。
すべりをsとすると、
n = \frac{120f}{p} \times (1-s)
となる。

問題に戻る。
公式より、
n = \frac{120 \cdot 66}{6} \times 0.95 = 1254 min^{-1}
となる。

Consideration.

極数とは何か、極数と1回転するための回数との関係が重要となる。
極数の半分の回数で1回転するのをイメージできるとよい。