制御工学part1 過渡応答 18th-day

Question.

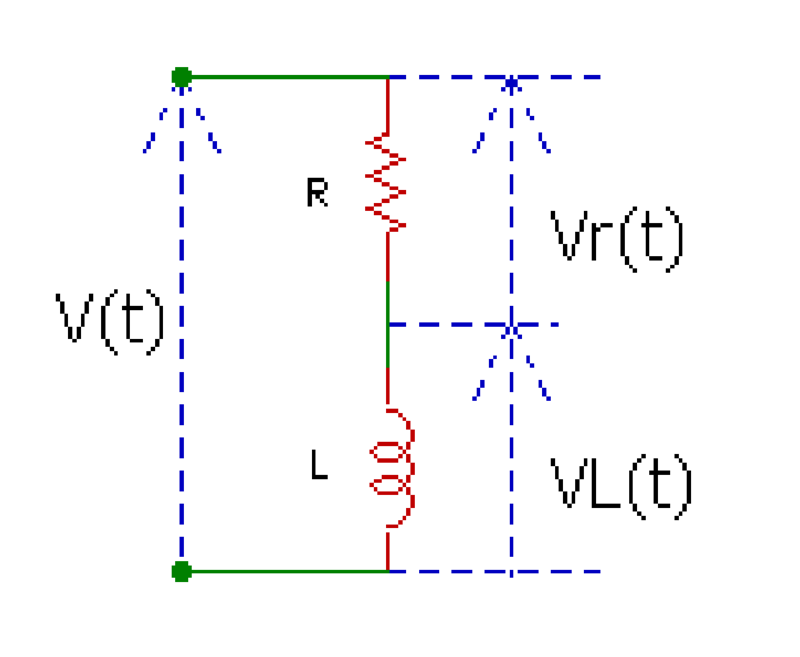
下図で構成される回路に、ヘビサイド関数に従った電圧v(t)を与える。
このときの電流i(t)の特性を求めよ。
f:id:meriyasu_blog:20150307130734p:plain:w200

Solver.

制御工学の基礎、過渡応答の問題である。
ただし、この問題は、電験3種では、出ない可能性が高い。

制御工学とは、

入力と出力の関係を示す伝達関数を用いることによって、
その入出力システムの挙動及び、パフォーマンスを評価するための学問である。

と定義される。
制御工学では、
時間領域に存在する、元となる方程式・入力信号をラプラス変換によって、
複素数領域に持ち込み、処理をしたのちに逆フーリエ変換を用いて、時間領域に戻すことによって、
出力の挙動を得ることができる。

複素数領域に持ち込む手法の一つであるラプラス変換とは、次式によって定義される。
${ F(s) = \int_{0}^{\infty}f(t)e^{-st}dt \\ ただし、s = \sigma + j \omegaとする。 }$
また、逆ラプラス変換は、次式によって定義される。
${ f(t) = \frac{1}{2 \pi j} \int_{c-j \infty}^{c+j \infty}F(s)e^{st}ds }$
これらの定義式を毎回使うのは、大変であるため、通常は、ラプラス変換表という表を用いて、計算を行う。
抜粋したフーリエ変換表をTable1に示す。

Table1. フーリエ変換表(一部抜粋)
	$f(t)$	$F(s)$
1	${ \delta (t) = \left\{\begin{array}{l} \infty \ \ \ t = 0 \\ 0 \ \ \ \ t \neq 0 \end{array}\right. }$ (インパルス関数)	$1$
2	${ u(t) = \left\{\begin{array}{l} t < 0 \ \ \ u(t)=0 \\ t \geq 0 \ \ \ u(t)=1 \end{array}\right. }$ (ヘビサイド関数)	$\frac{1}{s}$
3	$e^{-at}$	$\frac{1}{s+a}$
4	$f'(t)$	$sF(s)-f(0)$
5	$\int_{0}^{t}f(t)dt$	$\frac{1}{s}F(s)$

これらを使い、変換していく。
では、回路素子について、ラプラス変換を考えていく。

抵抗のラプラス変換

抵抗は、オームの法則より、以下の式で表される。
$v(t) = R \times i(t)$
よって、フーリエ変換を行うと、
${ \left\{\begin{array}{l} V(s) = R \times I(s) \\ I(s) = \frac{1}{R} \times V(s) \end{array}\right. }$
となる。

容量のラプラス変換

キャパシタの関係式は次のようにあらわされる。
$v(t) = \frac{1}{C} \times q(t)$
また、電流は微小時間当たりの電荷量であるので、
$i(t) = \frac{dq(t)}{dt}$
よって、
$i(t) = C \frac{dv(t)}{dt}$
$v(t) = \frac{1}{C} \int i(t)dt$
v(t)をラプラス変換表5番によって、ラプラス変換すると、
$v(t) = \frac{1}{C} \int i(t)dt \Leftrightarrow V(s) = \frac{1}{sC} I(s)$
$I(s) = sCV(s)$
となる。

インダクタのラプラス変換

インダクタの定義式は、
微小時間当たりの電流の変化量が電圧に比例し、比例定数をLとするので、
$v(t) = L \frac{di(t)}{dt}$
v(t)をラプラス変換表4番によって、ラプラス変換すると、
$v(t) = L \frac{di(t)}{dt} \Leftrightarrow V(s) = sLI(s)$
$I(s) = \frac{1}{sL}V(s)$
となる。

電気回路における出力信号の求め方を説明する。

回路方程式を求める
回路方程式をラプラス変換により、複素数領域に持ち込む
入力信号をラプラス変換により、複素数領域に持ち込む
回路方程式と入力信号を複素数領域において、掛け合わせる
逆ラプラス変換によって、時間領域に戻す

このような手順で出力を求めることができる。
では、早速、順番通りに解いていく。

回路方程式

直列RL回路の電圧を考える。
抵抗による電圧降下 $v_r$ は、
$v_r (t) = R \times i(t)$
インダクタによる電圧降下 $v_l$ は、
$v_l (t) = L \frac{di(t)}{dt}$
よって、起電力 $v(t)$ は、
$v(t) = v_r + v_l = R i(t) + L \frac{di(t)}{dt}$

回路方程式のラプラス変換

さきほどの抵抗とインダクタのラプラス変換を用いて、ラプラス変換を行うと、
${ v(t) = R i(t) + L \frac{di(t)}{dt} \\ \Leftrightarrow V(s) = \mathcal{L}[Ri(t)] + \mathcal{L} \left[L\frac{di(t)}{dt} \right] = RI(s) + sLI(s) = (R+sL)I(s) }$
よって、
$I(s) = \frac{1}{R+sL} V(s)$

入力信号のラプラス変換

入力信号は、ヘビサイド関数であるため、
ヘビサイド関数を $u(t)$ とおくと、そのラプラス変換は、
$\mathcal{L}[u(t)] = \frac{1}{s}$
となる。
$t \geq 0$ のときの電圧値を $V_0$ とすると、
$\mathcal{L}[V_0 \times u(t)] = \frac{V_0}{s}$
となる。

複素数領域での回路方程式と入力信号の融合

入力電圧信号を回路方程式に代入する。
つまり、 $V(s) = \frac{V_0}{s}$ である。
そして、逆フーリエ変換しやすい形へと変形していく。
${ I(s) = \frac{1}{R+sL} \times \frac{V_0}{s} = \frac{V_0}{sR+s^2 L} \\ = \frac{V_0}{s(R+sL)} = \frac{V_0}{L} \times \frac{1}{s \left(\frac{R}{L}+s \right)} }$
ここで、部分分数分解を行う。
${ \frac{1}{s(\frac{R}{L}+s)} = \frac{A}{s}+\frac{B}{\frac{R}{L}+s} \\ \frac{A \frac{R}{L} + As + Bs}{s \left(\frac{R}{L}+s \right)} }$
よって、
${ \left\{ \begin{array}{l} A \frac{R}{L} = 1 \\ A + B = 0 \end{array} \right. }$
となり、
${ \left\{ \begin{array}{l} A = \frac{L}{R} \\ B = - \frac{L}{R} \end{array} \right. }$
となるので、
${ \frac{1}{s(\frac{R}{L}+s)} = \frac{L}{R} \left(\frac{1}{s} - \frac{1}{s+\frac{R}{L}}\right) }$
したがって、
$I(s) = \frac{V_0}{R} \left(\frac{1}{s} - \frac{1}{s+\frac{R}{L}}\right)$
ここで、 $\frac{V_0}{R}$ 及び、 $\frac{R}{L}$ は定数であるので、
フーリエ変換表2, 3番を用いて、逆フーリエ変換を適用できる。
${ i(t) = \frac{V_0}{R} \left(\mathcal{L}^{-1} \left[\frac{1}{s} \right] - \mathcal{L}^{-1} \left[\frac{1}{s+\frac{R}{L}} \right]\right) \\ = \frac{V_0}{R}(1-e^{-\frac{R}{L}t}) }$

f:id:meriyasu_blog:20150307214004p:plain:w300

Consideration.

今回は、制御工学基礎・ラプラス変換についての問題であった。
ラプラス変換の最大の利点は、複素数領域に持っていくことで、
出力を考えるときに難しい計算を行わなくてよくなるという面である。
複素数領域で計算された値自体には意味はないが、それを逆ラプラス変換によって、
出力信号という意味のある式を導き出すことができる。

しかし、これは、制御工学の本質ではなく、本質は、伝達関数である。
伝達関数については、のちほど。

Memorandums?

This blog is written about technical-discoveries and daily-events.